最大似然估计（Maximum likelihood estimation, MLE） 和 最大后验概率估计（Maximum a posteriori estimation, MAP） 是很常用的两种参数估计方法。本文将详解MLE和MAP的思路和区别。

原创不易，转载请注明作者及出处： Whispery的闲庭小室

作者：Whispery

原帖地址：https://whispery.top/2024/03/详解极大似然估计和最大后验估计/

在此之前

概率与统计

首先我们要搞清楚MLE和MAP到底是什么方法，研究什么问题，用途是什么。而在此前要了解概率和统计的区别。

概率和统计是关系密切的概念，但是两者对问题的关注方向不同。

网上关于两者的关系和区别有很多说法和比喻，我在这里说一下我个人的理解： 概率关注问题的结果，统计关注问题的过程。

比如说，我有一个随机数生成器，它的原理是以某种特定的方法生成0或1，概率学会关注生成0或1的概率，而统计学会关注生成结果的方法——也就是生成随机数的过程。

上面的例子可能还是有点绕，不如更现实一些。例如学校课堂上老师用座位表随机点人，问题是我会不会被老师点到，那么概率学会关注我有多少可能会被点，而统计会关注老师点人的习惯特点（例如老师因为右手拿座位表手指会挡住一些人名导致那个位置的人几乎不会被点）

回到MLE和MAP上，MLE和MAP是统计领域的问题，这两种方法能够根据统计估计假设模型中的参数。

贝叶斯定理

在了解MLE和MAP之前，你还得了解 贝叶斯定理（Bayes’ Theorem） ：

$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$

别慌，贝叶斯定理其实是条件概率和联合概率公式推来的。

我们可以浅显的从现实去看这个公式——假设在小区的白天，电动车响了，会不会是有人在偷车？令有人在偷车为事件A，电动车响了为事件B。等式左边， $P(A|B)$ 表示电动车响是有人在偷车的概率；等式右边， $P(B|A)$ 表示有人偷车的时候电动车响了， $P(A)$ 表示有人在偷车， $P(B)$ 表示电动车响了。

当电动车发出声响的时候，大部分人都不会觉得是有人在偷车，为什么呢？因为我们知道：虽然 $P(B|A)$ 偷车的时候电动车会响的概率很大，但是有人偷电动车这一事件发生 $P(A)$ 的概率本身会较小，而且同时 $P(B)$ 电动车会响的事情会很大——电动车发出响声再平常不过了。因此总体而言 $P(A|B)$ 的概率就小了，也就是电动车响了的时候有人在偷车的概率小了。

回到公式上，贝叶斯定理描述了 在考虑事情本身发生及其前提发生的可能性后，发生的概率会有多大？ ，或者说： 你有多大把握相信一件事会发生。

还不理解？不妨将上面那个例子设置得极端一些：假如说世道混乱，~~民风淳朴~~，你觉得偷电动车再常见不过，那么在你眼里 $P(A)$ 有人偷电动车的概率很大，那么 $P(A|B)$ 总体就会更大了。又或者小区里的电动车都很乖，平时正常使用都不怎么响的，那么 $P(B)$ 电动车响声的概率就很小，总体而言 $P(A|B)$ 总体就会更大，当响声时你也会觉得是不是有人在偷车。又或者知道电动车的警报系统很拉跨，很多时候即使有人偷车也不会响，那么 $P(B|A)$ 很小，那么总体而言 $P(A|B)$ 变小，偶尔响一下也不会觉得是有人在偷车，因为觉得大部分小偷偷车的时候都不响，警报系统没有可信度，现在响也不能证明有人在偷车。

这就是我关于现实视角下的贝叶斯定理的解释和理解。

似然函数

极大似然估计（MLE），我们可以猜，极大就是最大值或者很大数的意思，而估计则可以从概率与统计中得到答案——估计模型的参数……那么，似然是什么？

为此，要说说似然函数。

在参考文章里，我找到了一个很好的解释。

似然（likelihood）这个词其实和概率（probability）是差不多的意思，Colins字典这么解释：The likelihood of something happening is how likely it is to happen. 你把likelihood换成probability，这解释也读得通。但是在统计里面，似然函数和概率函数却是两个不同的概念（其实也很相近就是了）。

对于这个函数（或者你可以理解为一个抽象没有具体形态的方程，描述了模型参数 $\theta$ 和结果 $x$ 的关系）：

$P(x|\theta)$

输入有两个： $x$ 表示某一个具体的数据； $\theta$ 表示模型的参数。

如果 $\theta$ 是已知确定的， $x$ 是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点 $x$ ，其出现概率是多少。

如果 $x$ 是已知确定的， $\theta$ 是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现 $x$ 这个样本点的概率是多少。

可以回到上面那个关于概率和统计那个随机数生成器的例子，生成器随机生成0和1，我们假设生成器用的是某种模型，然后模型通过一个参数 $\theta$ 随机生成0和1。那么当 $\theta$ 已知时，令生成的结果 $x$ 为变量，这时候 $P(x|\theta)$ 就是概率函数，描述了0和1出现的概率分布。而当 $x$ 已知时，令 $\theta$ 为变量，这时候 $P(x|\theta)$ 就是似然函数，其表述了在生成器设置不同的参数 $\theta$ 下，已知的 $x$ 出现的概率。

MLE与MAP

最大似然估计 MLE

终于要写这部分了。

想象面前有两个箱子，一个箱子装满了红球，一个箱子装满了白球。

再想象我们有台机器，它会按照随机地从两个箱子里抽出一个球。

我们先假设一个简单的模型来描述这个过程：

$f(x)=\begin{cases} 机器选择抽红球, & \theta > x > 0 \\ 机器选择抽白球, & 1 > x > \theta \end{cases}$

机器产生从0到1的随机数x，然后判断 $x$ 是比 $\theta$ 大还是小来决定是抽红球还是白球。

问题来了，我们怎么找到最切合实际的模型参数 $\theta$ 呢？

答案是通过实际实验来找。

那么现在开始抽球，让机器抽了10个球，实验结果 $x_0$ 是：红白红红白红白白红红。

回到先前那个奇怪的函数 $P(x|\theta)$ ，在抽象层面上，现在我们知道了结果 $x$ ，可以通过这个函数（方程）求出 $\theta$ ——不过在此之前，我们要先求出这个函数在当前问题下的具体形式才能进行求解——也就是求出出现实验结果 $x_0$ 的似然函数。

根据上面假设的模型，我们知道这是简单的几何概型（不知道几何概型也没关系），抽出红球的概率是 $\theta$ ，抽出白球的概率是 $1-\theta$ ，那么出现结果 $x_0$ 的似然函数可以简单的推导出来：

$P(x_0|\theta)=\theta\times(1-\theta)\times\theta\times\theta\times(1-\theta)\times\theta\times(1-\theta)\times(1-\theta)\times\theta\times\theta$

化简得

$P(x_0|\theta)=\theta^6(1-\theta)^4$

这就是结果为 $x_0$ 时关于变量 $\theta$ 似然函数， $\theta$ 在我们假设的模型中则是模型的参数，我们可以画出函数图来看一下这玩意长什么样。

函数图像

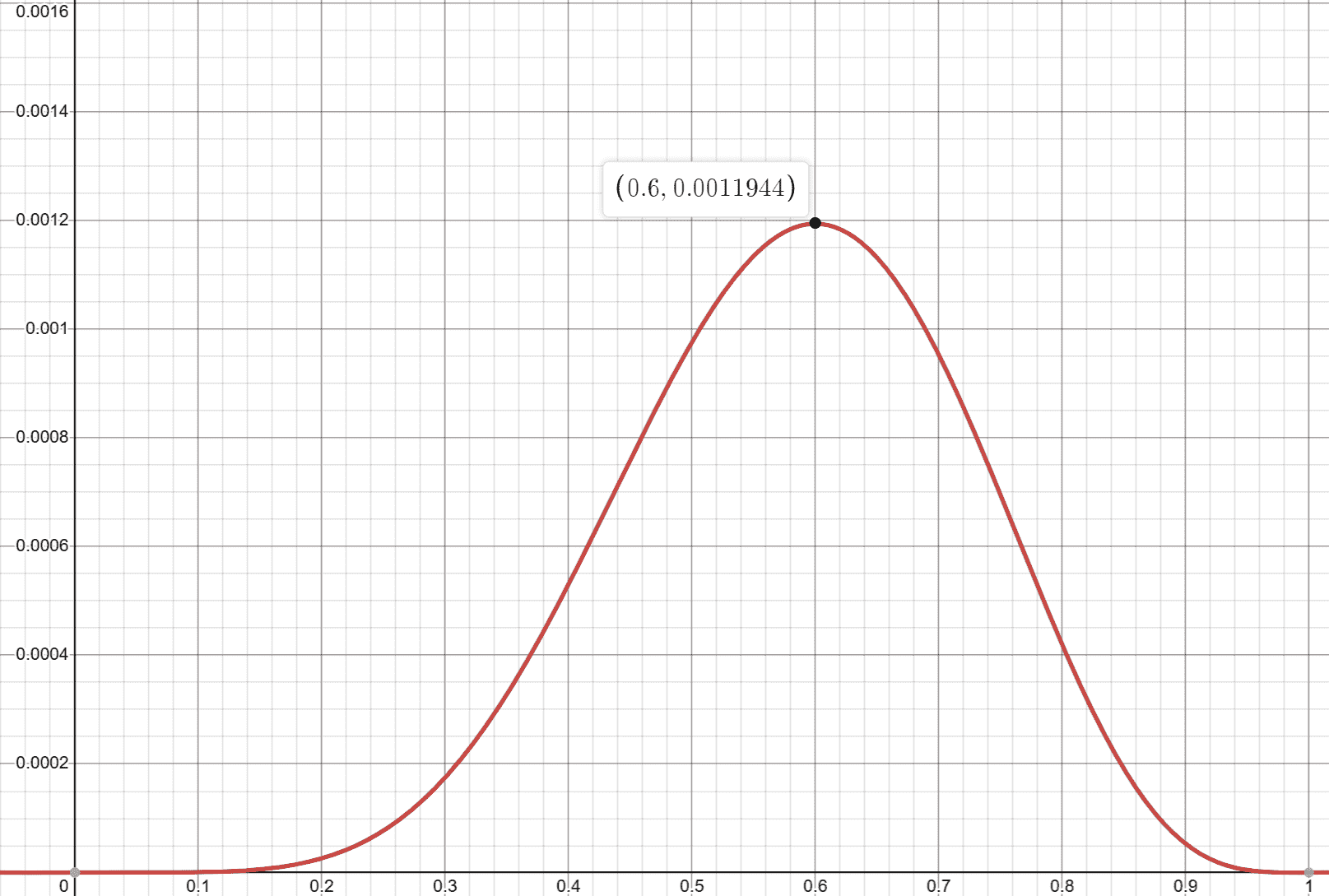
长这样。

横轴是 $\theta$ ，而纵轴则是 $P(x_0|\theta)$ ，也就是在不同 $\theta$ 下出现抽球结果 $x_0$ （注意在上面的求似然函数的过程中，我们考虑了全部十次抽球结果， $x_0$ 代表了十次结果整体而不是分开的一次次结果）的概率。

我们可以发现，当模型参数 $\theta$ 为 $0.0011944$ 时，抽球抽出结果 $x_0$ 的概率最大。

也就是说，我们模型里的参数 $\theta$ 为0.0011944时，最贴合实验结果 $x_0$ 。通过似然函数和已知的实验结果，求似然函数最大值对应的 $\theta$ 的方法，我们知道了给模型取什么样的参数 $\theta$ 最能贴合实验结果的方法，这个方法就是最大似然估计MLE。

最大后验概率估计

好消息，~~在特异能力者对机器的读心实验中~~，我们知道了更多关于这台机器的情报，我们知道模型参数 $\theta$ 更有可能会是0.3——我们得到了关于 $\theta$ 的概率分布函数 $P(\theta)$ ，这个函数告诉了我们实际的 $\theta$ 有可能会是什么，也就是“ $\theta$ 等于某个数x”成立的概率，根据情报，我们知道了 $P(\theta)=\frac{1}{\sqrt{2\pi}a}\exp\left(-\frac{\left(x-b\right)^{2}}{2a^{2}}\right)$ 。

长这样：

函数图像

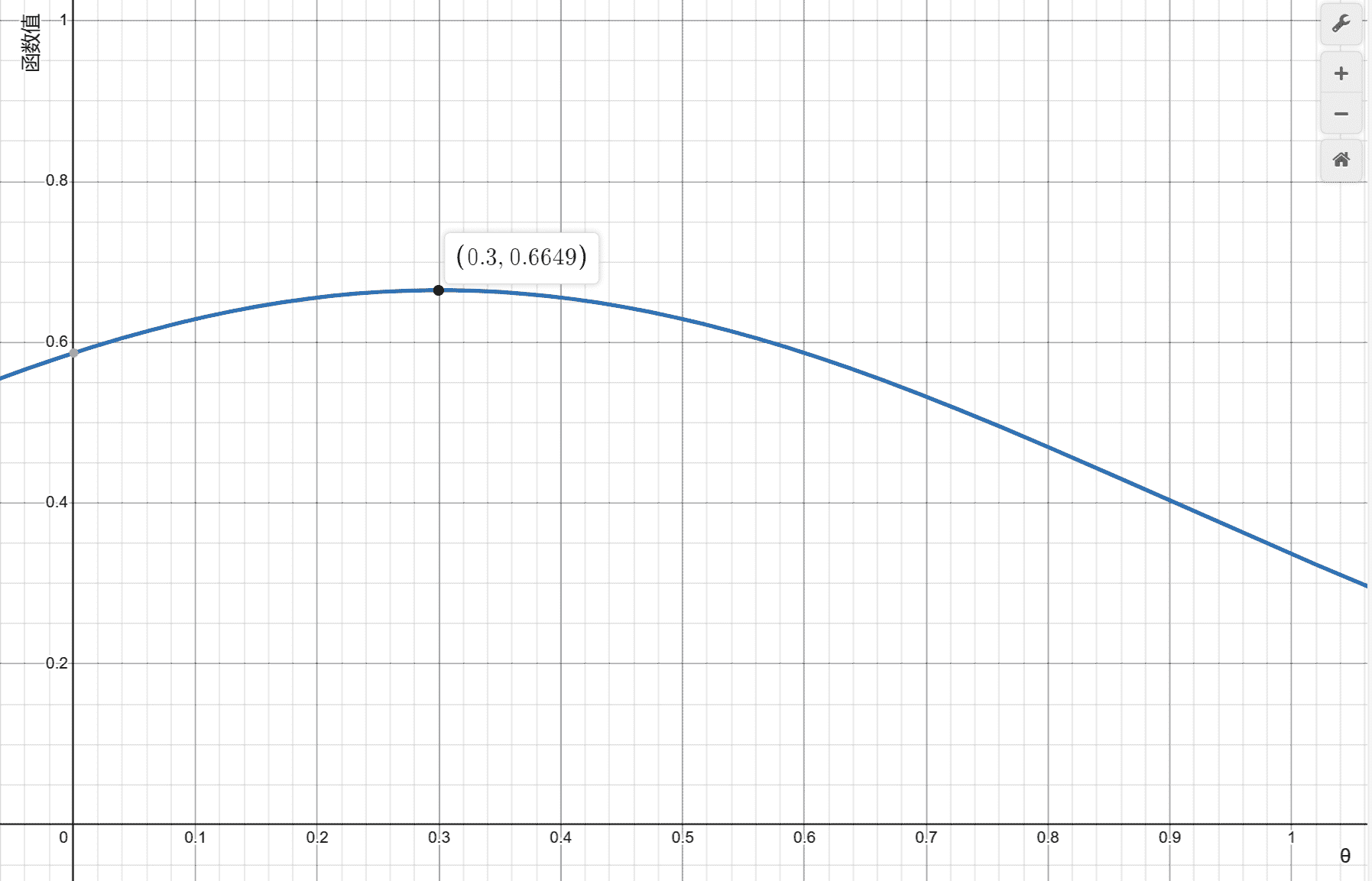
好吧这里面有很多槽点和漏洞，但是让我们别管它们！

我们该怎么把新得到的情报引入我们的最大似然估计呢？答案是贝叶斯定理！在考虑事情本身发生及其前提发生的可能性后，发生的概率会有多大？——我们不只参考了实验结果，也参考了 $\theta$ 本身等于某个数的概率 $P(\theta)$ 。

在最大似然估计中，我们通过取最大 $P(x|\theta)$ 来获得最切合的模型参数 $\theta$ ，我们可以用条件概率表示 $P(\theta|x)$ 当实验结果为x时参数为 $\theta$ 的概率。

根据贝叶斯定理，可知：

$P(\theta|x)=\frac{P(x|\theta)P(\theta)}{P(x)}$

当 $P(\theta|x)$ 函数值最大的时候，也就是 $\theta$ 最有可能取得的数。因此我们找到 $P(\theta|x)$ 最大时对应的 $\theta$ 就可以求得在考虑了新情报的情况下最合适实验结果的 $\theta$ 。

在实际问题中我们已知实验结果，变量时 $\theta$ ，因此 $x$ 为定量，则 $P(x)$ 也为定量，因此想找等式左边的最大值，只需要关注右边分子的最大值，问题变成了找 $P(x|\theta)P(\theta)$ 最大时对应的x。

在前面我们知道了 $P(x_0|\theta)=\theta^6(1-\theta)^4$ ，根据后来的情报我们又知道了 $P(\theta)=\frac{1}{\sqrt{2\pi}a}\exp\left(-\frac{\left(x-b\right)^{2}}{2a^{2}}\right)$ ，那么 $P(x|\theta)P(\theta)$ 不就是将两者乘起来了嘛！通过计算机轻松画出函数图像找到最大值。（其实在实际计算中不用画图像也能求最大值）

后验概率

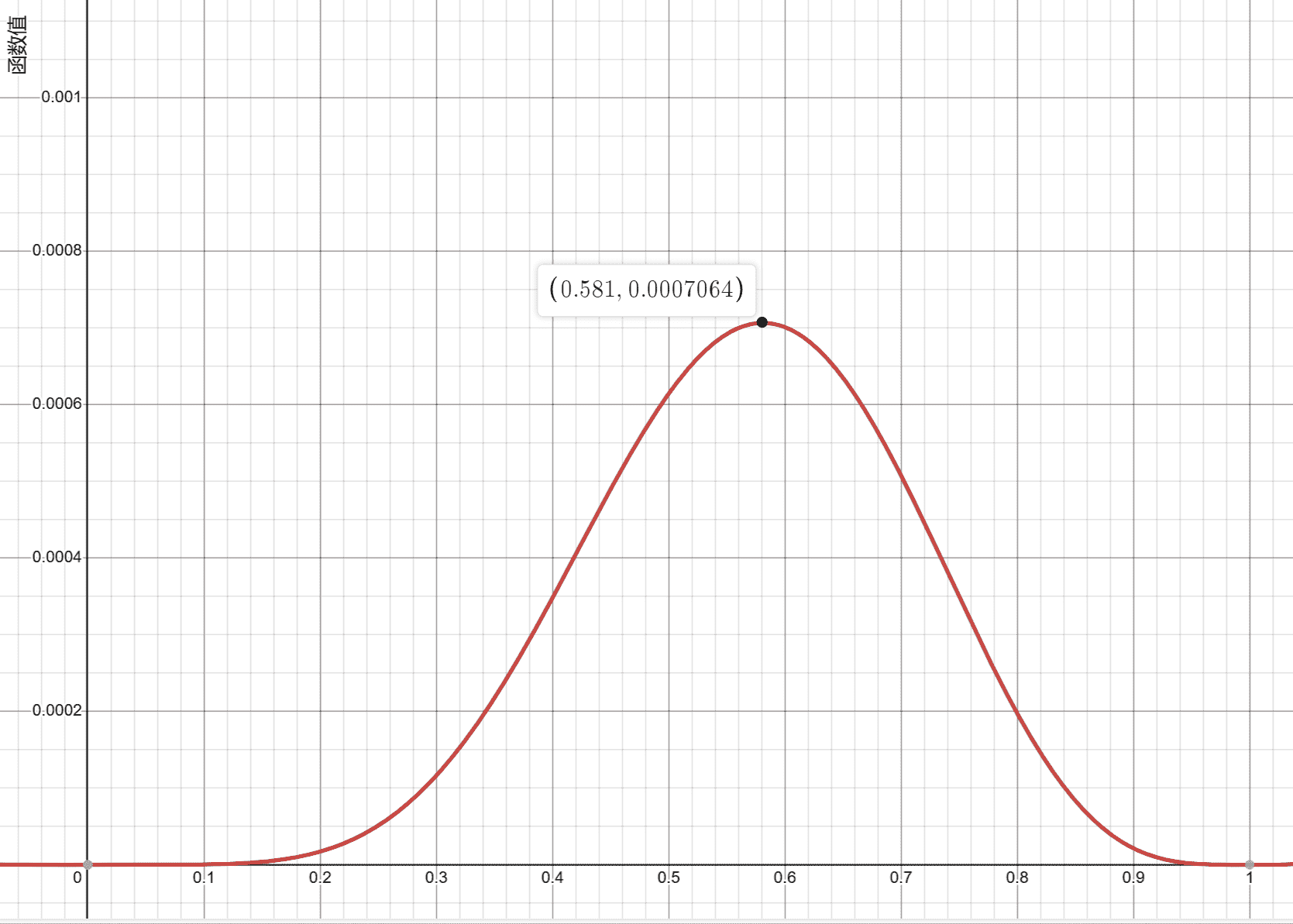
我们可以找到函数最大时 $\theta$ 对应的值： $0.581$ 。

这就是考虑了新情报以后最切合实验结果的模型参数。

回到上面的公式 $P(\theta|x)=\frac{P(x|\theta)P(\theta)}{P(x)}$ 上，根据先验概率和后验概率的定义，我们知道在公式中， $P(\theta)$ 是先验概率，而 $P(\theta|x)$ 是后验概率。在我们上面求最切合的模型参数的方法里，我们把求最切合模型参数的问题转换成了求解后验概率 $P(\theta|x)$ 的最大值的问题——这就是“最大后验估计”。

后话

需要知道的是，不管是最大似然估计还是最大后验估计，我们都是在求我们所假设的模型的最佳参数，由于模型本身是假设的，所以结果可不可靠除了参数以外，也要选择切合实际的模型。在上面的例子中，万一机器抽球原理不是我们假设的模型而是其他的呢？

而在最大后验估计中，“新情报”（也就是先验概率）的可靠程度也影响了最大后验估计的结果，有时候不一定是什么都加入考虑加入计算就能得出最贴合实际的模型和参数。同样还是上面那个例子，如果异能者为了拖延我们对机器的研究，故意造假给出了先验概率 $P(\theta)$ 呢，那么我们的计算结果就会受到假信息的干扰，从而难以得到正确的结果。

~~或许我们应该调查一下那一名异能者。~~

参考文章

详解最大似然估计（MLE）、最大后验概率估计（MAP），以及贝叶斯公式的理解